

Fair sharing
The first probability problems that Blaise Pascal and Pierre de Fermat studied (beginning in 1654) concerned gambling. We will present a modern version of a similar problem with three different solutions.
Two gamblers bet on the outcome of a contest between two teams, A and B. Winning the contest meant to win 3 out of 5 games. Each gambler put in $300, so the total bet was $600. Team A won the first two games. But due to a natural disaster, no more games were played. How should the money be divided? And why is it fair?
The first solution: Each gambler gets back his/her original $300.
Reasons for this solution: There were still two possibilities left. Each team still could win. So each gambler should get the same amount. Also, "When everyone gets the same amount, noone has a reason to complain."
A reason against this solution: The gambler who had a better chance to win when the match was interrupted should get more money, but how much more is a matter of opinion.
The second solution assumes a fixed probability (Pascal and Fermat):
The gambler who bet on team A should get $525, and the other gambler should get only $75 (a 7/8 : 1/8 split).
Reason for: Assume that the probability that a team wins a game is ½. So if the match had not been interrupted, one of the following outcomes would have happened:
Outcome: Probability: (W means "team A wins")
W W W 1/2
W W L W 1/4
W W L L W 1/8
W W L L L 1/8 team B wins the contest!
The ratio of the probabilities of winning for the two teams A and B were 7/8 to 1/8, so this ratio should be used in dividing the money.
Reason against: A probability of winning is not a fact. It is an expectation or belief. There is no reason to give more money to a gambler because the gambler and other people believe that the gambler will win.
The third solution estimates the probability depending on the performance. (Bookies' method: if the score is n : n or n : n-1, the probability of the next win is 1/2. But if the score is n : m where m < n-1, the probabilities of winning by the two teams are
n/(n+m+1) and (m+1)/(n+m+1). )
So the probability of A winning changes, depending on the previous outcomes:
Situation: Probability that
A wins: A loses
W W 2/3 1/3
W W L 1/2 1/2
W W L L 1/2 1/2
Probability of possible outcomes, given that team A has won two; the contest continues until one team has won 3 out of 5 games (see the tree structure below for an explanation)
Outcome: Probability:
W W W 2/3
W W L W 1/6
W W L L W 1/12
W W L L L 1/12 team B wins the contest!
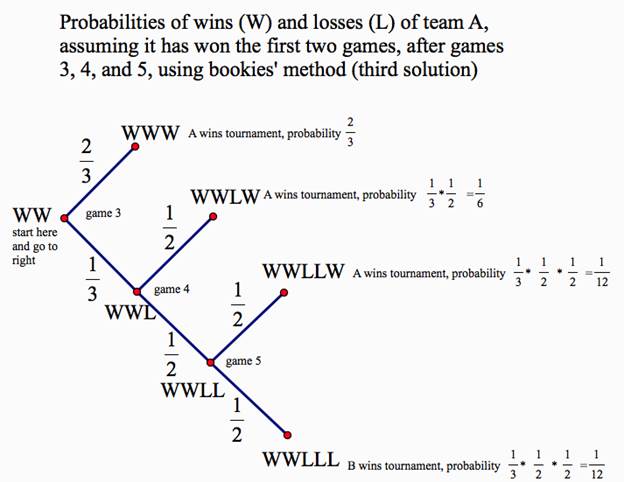
Thus one gambler gets $550 and the other gambler gets only $50.
The reason for: This ratio (11:1) corresponds better to the observed frequencies of winning such contests than does the ratio (7:1), which is used in the second solution.
The reason against: "When you are already getting more, don't get greedy!"
So, which method is fair?